北見市で開催した「子育て講座」の続きです（今回で最後にします）。

「我が子の学力は小１で決まる」というテーマでした。

これは今のところ本当だと思います。

「今のところ」というのは現在の社会制度下ではという意味です。

ですから、小１のお子さんを持っている保護者の方のためにこの講座を開きました。

小１を担任されている学校の先生方にもお役に立てたら幸いです。

１．親は怖くて教えられない

参加されたお母さん方に「さくらんぼ計算」をやっていただきました。

どういう順番で教えるか？

という問題です。

お母さん方は悩みました。

悩んだ末に、「３と５に分ける派」と「７と３で10をやる派」に分かれました。

その結果、こんな言葉が聞かれました。

小学校１年生の問題でも親は怖くて教えられない

「さくらんぼ計算」でさえ、教え方に迷います。

ということは、間違った教え方（先生と違う教え方）をしてしまう可能性があるということです。

だから、怖くて教えられないという声が聞かれました。

そうなんです。

それが普通なんです。

つまり、

学校の先生は一般の方々が持っていない「教え方」を持っている

ということです。

それが専門職ということですね。

では、どうやって教えるのかを見て行きましょう。

２．「さくらんぼ計算」の教え方

「まんまるおはじき」で考えてみましょう。

７＋８に合わせて、おはじきを置きます。

この時に、一年生たちは「不思議な力」を使います。

７のおはじきを見る時に「不思議な枠」が出てくるのです。

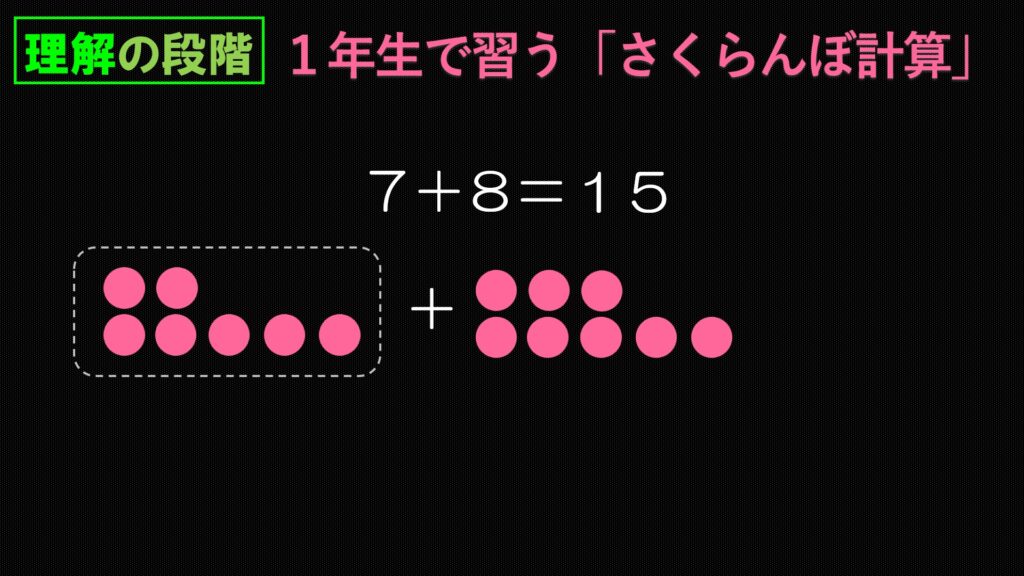
「不思議な枠」が出て来ましたね。

これを「10になる数」と言います。

この枠が出てくると、７が不自然に見えて来ます。

何かもの足りない。

「７が好きな数字」というのがあるんです。

そうです。

７は３が好きなのです。

そこで、隣の８からおはじきを３個もらってしまいます。

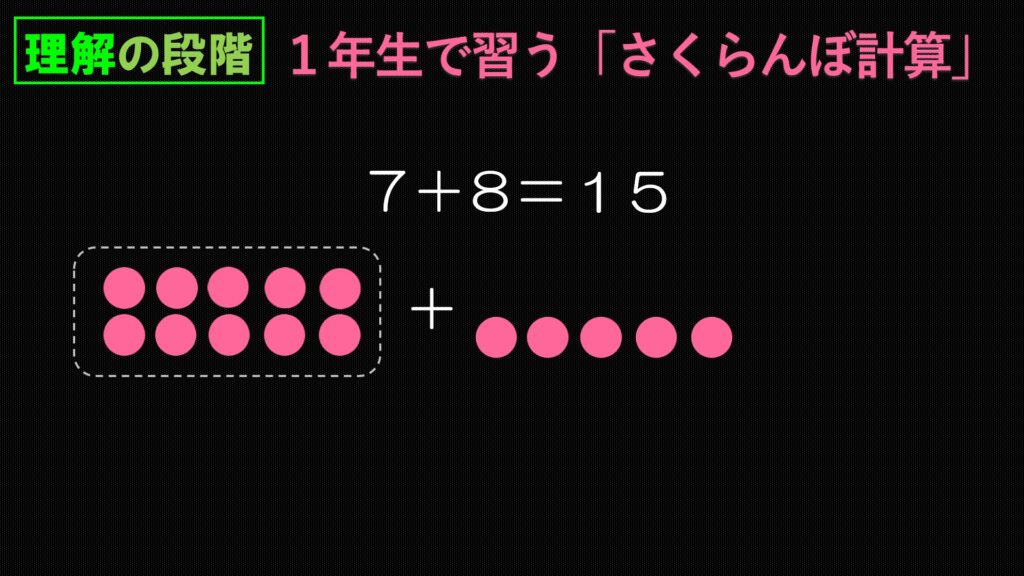
隣から３個奪って１０を作りました。

これで一安心です。

ここまでの作業を言語化します。

できるだけ短い言葉で、リズムよく、作業を言語で定型化させます。

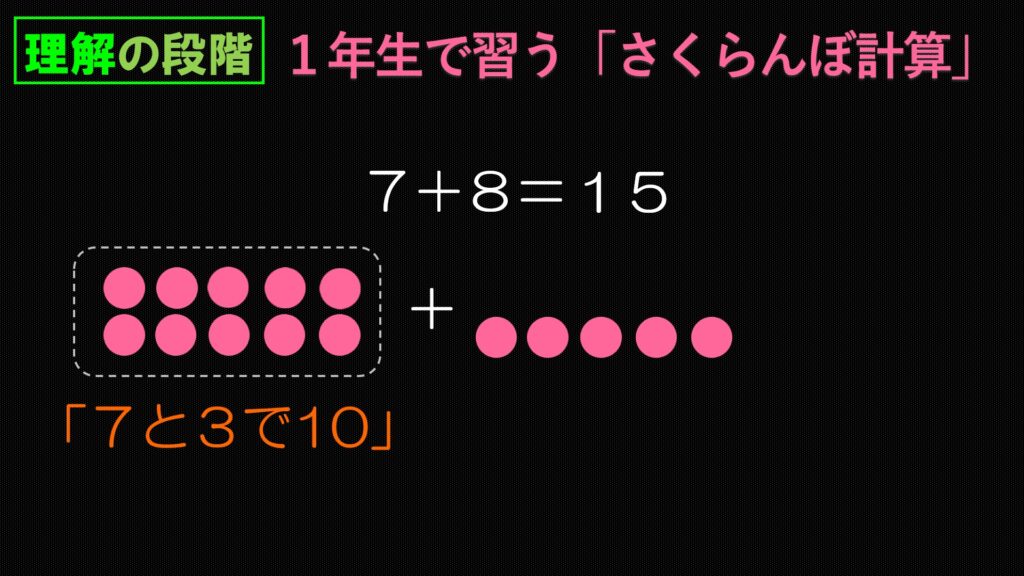
はい、できました。

「７と３で１０」です。

これを「10になる数」とか「10の補数」とか「10の合成」と言います。

実は、一年生は足し算を習う前にこうした勉強を何度もくり返しやっています。

見通しを持っているベテランの先生は、４月から算数の最初の５分くらいを使って毎回唱えさせています。

そうすると子どもたちは「７」という数字を見ただけで「３」をくっつけたくなってうずうずします。

５月のゴールデンウイークを待たないうちに、先生が「なな！」と口にしただけで「７と３で１０！」と声をそろえて答えられるようになります。

これを「自動化」と言います。

でも、こんな大切なことを大学では習いませんし、教師用指導書にも載っていません。

経験のある先生がどこかで伝えていかなければならないわけです。

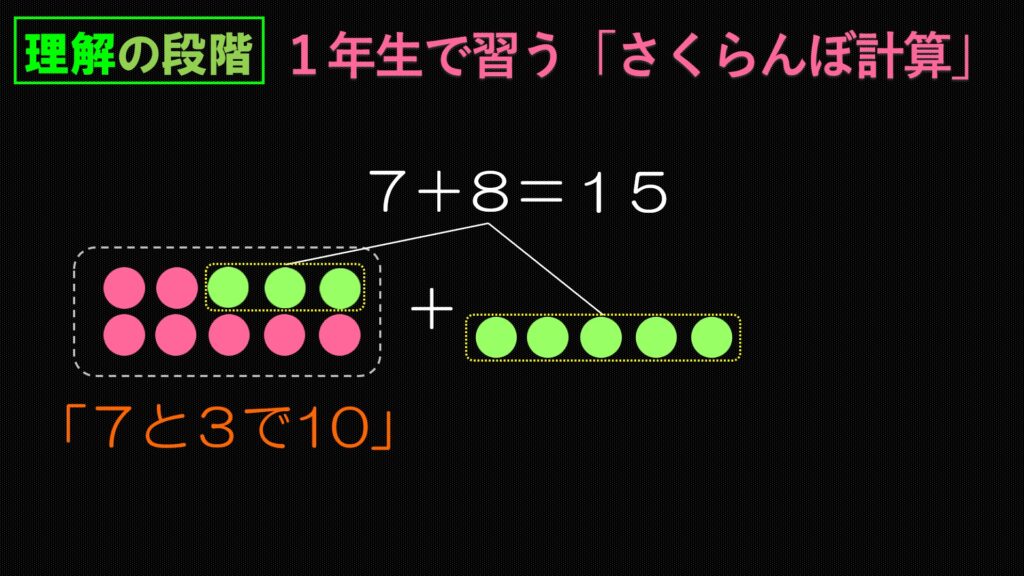
さて、８は３個取られちゃったわけですから、３と５に分解されたことになります。

この過程も言語化しておきます。

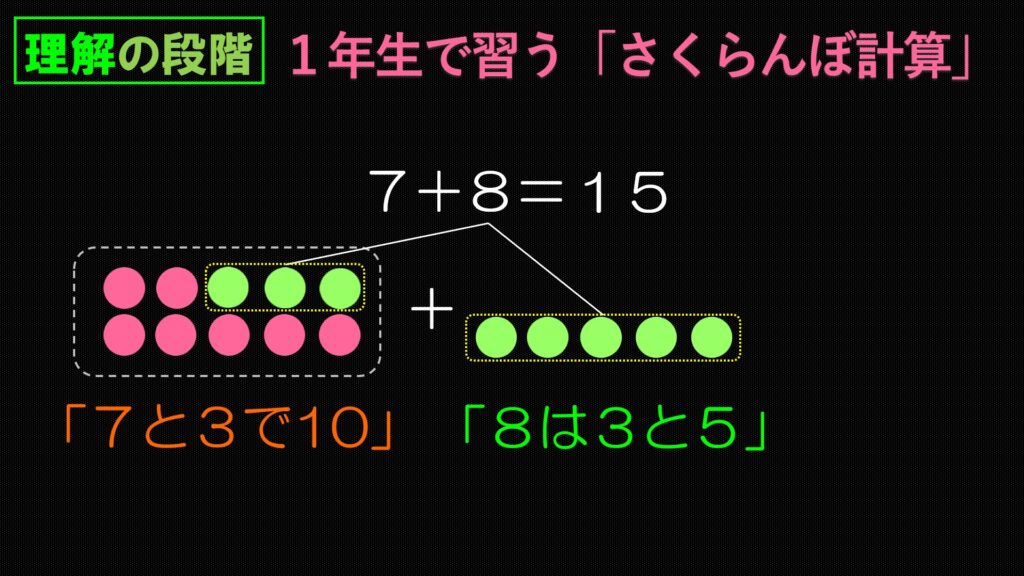
「８は３と５」です。

これも「数の分解」と言って、足し算を習う前にたくさん経験して来たことです。

ということで、子どもたちにとって足し算はそれほど難しくないことなのです。

ただし、それは、ここまでの作業が自動化・言語化されていればの話です。

ということで、この原理が理解できていれば「さくらんぼ計算」も難しくはありません。

最初にするのはこの部分です。

「８」は「１と７」「２と６」「３と５」「４と４」と分解方法がいくつかあります。

でも、最初は「７」にフォーカスするわけです。

そうすると「７が好きなのは３」ですから「７と３で１０」という作業をおこないます。

作業したことを書き残すことはワーキングメモリを助けます。

あとは後半です。

「８は３と５」を作業化して書き残します。

答えを書く時は、10と使っていない５を足して「答え１５」というわけです。

３．「自動化」までの三段階

さて、ここまでは「７＋８」という足し算のやり方を理解したに過ぎません。

図にするとこうなります。

四則計算の技能というのは10歳が臨界期を言われています。

教えてもらった知能が技能として無意識に使えるようになるのは10歳までが勝負ということです。

その四則計算の技能化（身体化）の最初が一年生で習う「くりあがりのない足し算」です。

まず、ここがいかに重要であるかを認識しておいてください。

次に、やり方がわかっただけで計算は出来ないということも認識してください。

計算というものはスラスラと出来なければならないのです。

自動化です。

意識しなくても自転車に乗れるようになるのと同じです。

そのために、教える側は「自動化の三段階」を知らなければなりません。

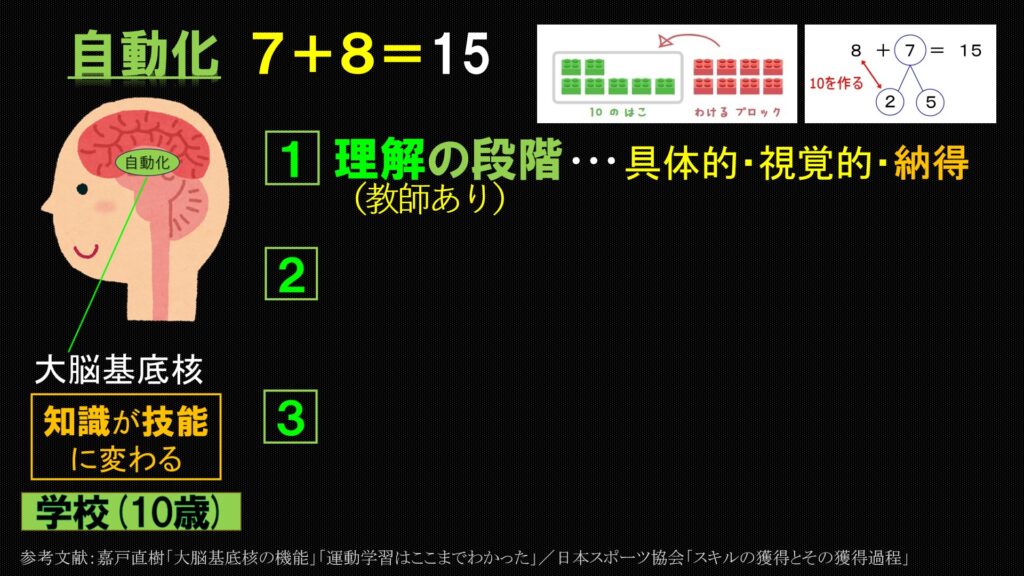
　理解の段階　→　練習の段階　→　自動化の段階

この３ステップで知識が技能に変わり脳の真ん中に無意識に取り出せる形で保存されるのです。

その第一段階（理解の段階）が、先ほど解説した「さくらんぼ計算」です。

理解の段階は別名「教師ありの段階」とも呼ばれます。

教師がやり方を教えることによって子どもが、

「わかった！」

となるのが理解の段階です。

そうなったら次は練習の段階です。

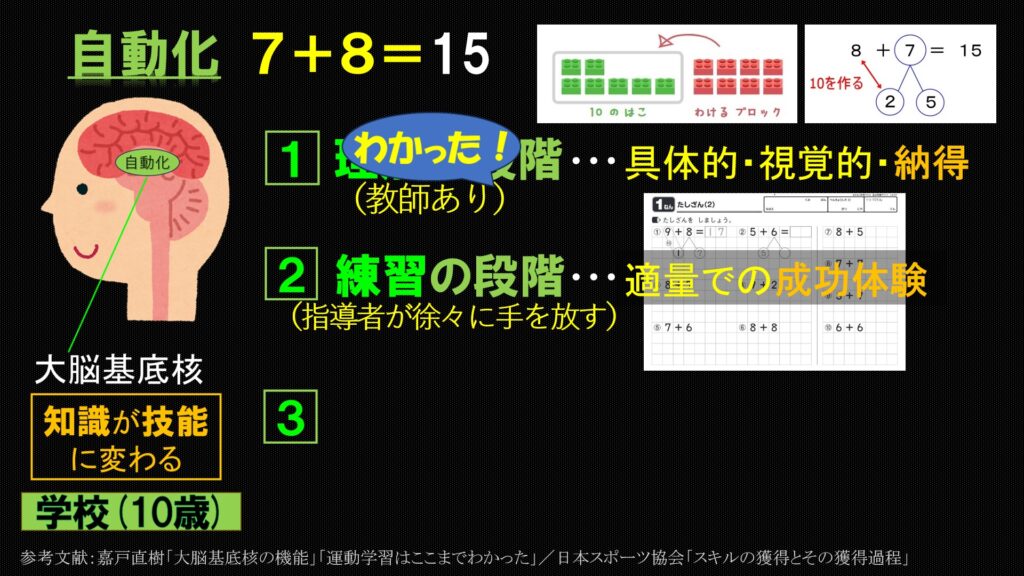
練習の段階では教師が徐々に手を放します。

子ども自身に練習させるということです。

ただし、いきなり手を放すのはダメです。

自転車の練習と同じです。

実は大人が少し支えてあげているのに、本人は自分の力でこいでいるような感じになるような支援です。

そうしていつの間にか自分だけで出来るようにさせるのが練習の段階です。

たとえばこれは「計算スキル」と呼ばれるものです。（画像は「あかねこ計算スキル」光村教育図書）

よく見てください。

徐々に手を放しているのがわかりますか？

①はさくらんぼ計算の仕方が書いてあります。

間違わせないためです。

転倒させない（失敗させない）。

成功体験をさせる。

それが練習段階初期の最重要課題なのです。

②はそれが途中までしか書いてありません。

③以降は「さくらんぼなし」です（自分で書かねばなりません）。

そういう配慮をしているのが「計算スキル」です。

まだあります。

①は答えが薄く書いてあります。

子どもはそれをなぞればマルをもらえます（成功体験）

お手本（やり方）を確かめさせて、少しずつ自分で出来るようにさせているのです。

答えの書き方を間違えないように答えの欄のマスも密かに書かれています。

そして、③以降は自分で「＝」も書かせます。

これが「徐々に手を放す」工夫です。

まだあります。

⑥と⑦の間に線が引いてありますよね。

これは「⑦～⑩は早く終わった子のための問題」です。

ゆっくりやる子は①～⑥だけでも100点です。

適量の練習で成功体験を重ねる

それが練習段階の最重要課題なのです。

あり得ないことですが、この計算スキルを宿題にする先生がいるようです。

絶対にダメです。

計算スキルは授業中に使います。

練習段階は「教師が徐々に手を放す段階」です。

教師がついていなければいけません。

励ましたり、そっと教えたり、学級という集団の中での緊張感を利用したりします。

その中で何が何でも全員に「成功体験」を味わわせる。

自分で出来た！やった！という実感を持たせる。

それが最重要課題ですから宿題にすることは絶対にありません。

「できた！」

これが練習段階のキーワードです。

ちなみに、「スキル」と似たような言葉に「ドリル」があります。

ドリルというのは、何度もくり返して練習させることを目的とした問題量の多い計算問題集です。

ですから、自習時間に使ったり、宿題に使ったりする先生が昔は多かったように思います。

それに対して「スキル」は授業中に使うもので、成功体験を目的にしています。

一見すると似ていますが思想が全く異なるものなのです。

そして、最後に自動化の段階です。

「教師なし段階」とも呼ばれます。

こうなれば、宿題でも構いませんし、親が面倒を見る必要もありません。

「さくらんぼ計算」は要りません。

「７＋８は？」と聞かれたら、考えることなく「１５！」と言える段階です。

畿央大学の森岡 周教授は「自動化」について次のように解説されています。

あらかじめ出力すべき明確な基準がないものであり，課題を繰り返すことで記憶が作られ，その記憶と実際の結果を結合していく相関学習過程のことである。（森岡周「脳科学からみた運動学習」理学療法学第38巻第8号2011年）

テニスで言えば、どこにサーブが飛んで来ても対応できる身体能力が出来た状態です。

親から突然、「７＋８は？」と言われて、「１５！」と即答できる状態です。

この段階になれば、文章問題に出会った時も、文章の読解に力を注ぐことができます。

お話しの意味が理解できれば計算技能を使うだけです。

「どっからでも来い！」という自信がキーワードです。

「できる！」

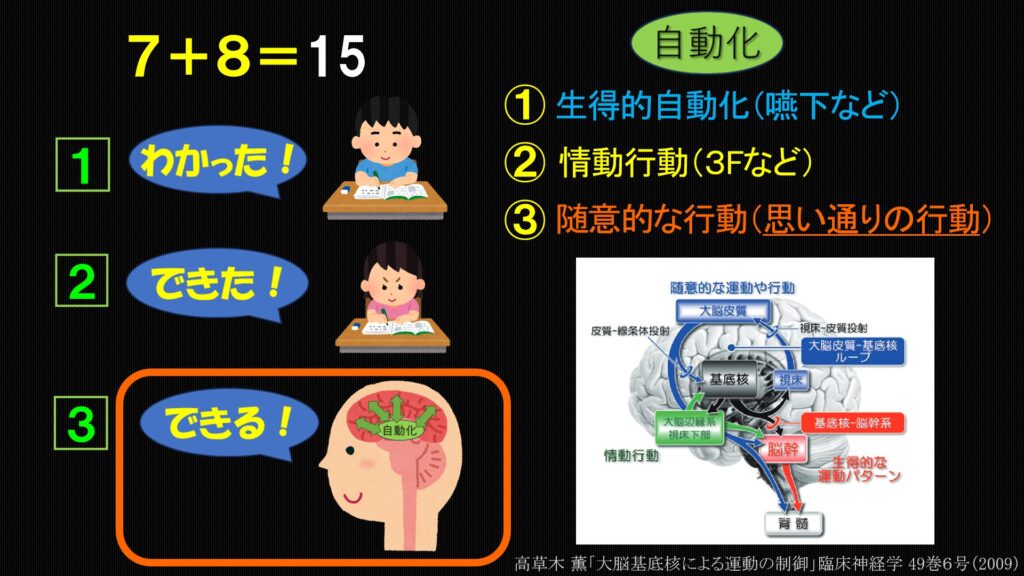
自動化にはいくつかの種類があります。

食べ物を食べた時に飲み込んだ物が気管の方に行かないように私たちの喉にはフタが付いています。

このフタは食べ物を飲み込んだ時に自動的に動きます。

これを生得的な自動化と言います。

二つ目は子どもの３Ｆ（防衛反応）などに見られる情動行動です。

幼児期に叱られてばかりいた子は自動的に「fight闘う」「flight逃げる」「freeze固まる」といった行動をとります。

「なんでそんなことするの！怒」と言われると、

「だって…」とか、「○○君も…」とかって、言い訳が自動的に出て来る子も同じです。

防衛反応が自動化されているわけです。

そして、三つ目が随意的な行動の自動化です。

随意的というのは「思い通りに出来る」という意味です。

自転車を思い通りに乗りこなせるのはこれです。

７＋８などのくり上がりのある足し算を即答できるのも随意的自動化です。

これができるためには脳の中の様々なネットワークを必要とします。

決して一朝一夕にできることではありません。

これ以上は有料のお話になるので今回はここで終わりにしておきます。

４．まとめ

小学校１年生の計算でさえ、親は怖くて教えられないという話をしました。

それだけ学校の先生は専門職だということです。

身近なようでいて「在れども視えず」の世界が学校なのです。

その一つの例として「くり上がりのあるたし算」を解説しました。

いくつもの行程があってけっこう複雑なのです。

そして、計算技能の習得までには「自動化の三段階」があることを解説しました。

　理解（わかた！）→　練習（できた！）→　自動化（できる！）

技能というのはこのように意図的計画的に見につけさせるわけです。

そして、それを組織的におこなっているのが学校という所です。

今回をもって「教え方三部作」を終わります。

【第一部】講座406　学校の先生方は「○○○」を知らない

【第二部】講座407　世間と教師の「教え方」の違い

【第三部】講座408　我が子の学力は小１で決まる